In diesem Abschnitt werden stationäre Strömungen kompressibler (dichteveränderlicher) Medien beschrieben. Es wird angenommen, dass dem Gas keine Wärme zu- oder abgeführt wird und dass keine Reibungsverluste auftreten. Da die Dichte der Gase klein ist, wird der Einfluss der Gravitation ebenfalls vernachlässigt.
Definitionen der Machzahl
Bezieht man die Strömungsgeschwindigkeit \(v\) auf die Schallgeschwindigkeit
\begin{equation}
a = \sqrt{\gamma R_{i} T}
\label{eq:sos1}
\end{equation}
erhält man die Machzahl
\begin{equation}
Ma = \frac{v}{a}
\label{eq:def_Ma1}
\end{equation}
Eine weitere Definition der Machzahl erhält man, wenn man die Geschwindigkeit auf die mit der Totaltemperatur \(T_{t}\) gebildete Schallgeschwindigkeit \(a_{t}\) bezieht:
\begin{equation}
a_{t} = \sqrt{\gamma R_{i} T_{t}}
\label{eq:sos2}
\end{equation}
\begin{equation}
Ma_{t} = \frac{v}{a_{t}}
\label{eq:def_Ma2_t}
\end{equation}
Zwischen \(Ma\) und \(Ma_{t}\) bestehen folgende Zusammenhänge:
\begin{equation}
Ma_{t}^{2} = \frac{Ma^{2}}{1 + \frac{\gamma – 1}{2} Ma^{2}}
\label{eq:Mat_aus_Ma}
\end{equation}
\begin{equation}
Ma^{2} = \frac{Ma_{t}^{2}}{1 – \frac{\gamma – 1}{2} Ma_{t}^{2}}
\label{eq:Ma_aus_Mat}
\end{equation}
Darüber hinaus kann eine weitere Machzahl gebildet werden, indem die Geschwindigkeit auf die kritische Schallgeschwindigkeit \(a^{*}\) bezogen wird:
\begin{equation}
a^{*} = \sqrt{\gamma R_{i} T^{*}}
\label{eq:sos3}
\end{equation}
\begin{equation}
Ma^{*} = \frac{v}{a^{*}}
\label{eq:def_Ma3_s}
\end{equation}
Hierbei wird der Fall \(Ma = 1\) als der kritische Zustand bezeichnet und die zugehörigen Größen werden mit einem \(*\) gekennzeichnet:
\begin{equation}
\frac{p^{*}}{p_{t}} = \left ( \frac{2}{\gamma + 1} \right )^{\frac{\gamma}{\gamma – 1}}
\label{eq:p_crit}
\end{equation}
\begin{equation}
\frac{T^{*}}{T_{t}} = \frac{2}{\gamma + 1}
\label{eq:T_crit}
\end{equation}
\begin{equation}
\frac{\rho^{*}}{\rho_{t}} = \left ( \frac{2}{\gamma + 1} \right )^{\frac{1}{\gamma – 1}}
\label{eq:rho_crit}
\end{equation}
Auch in diesem Fall läßt sich zwischen \(Ma\) und \(Ma^{*}\) umrechnen:
\begin{equation}
Ma^{*2} = \frac{\frac{\gamma + 1}{2} Ma^{2}}{1 + \frac{\gamma – 1}{2} Ma^{2}}
\label{eq:Mas_aus_Ma}
\end{equation}
Abhängigkeiten der Größen untereinander
Die strömungsmechanischen Größen lassen sich jeweils in Abhängigkeit von nur einer anderen Größe angegeben, z.B. als Funktion des Druckverhältnisses \(p/p_{t}\):
\begin{equation}
Ma = \sqrt{\frac{2}{\gamma – 1} \left [ \frac{1}{\left ( \frac{p}{p_{t}} \right )^{\frac{\gamma-1}{\gamma}}} – 1 \right ] }
\label{eq:Ma_ppt}
\end{equation}
\begin{equation}
\frac{T}{T_{t}} = \left ( \frac{p}{p_{t}} \right )^{\frac{\gamma-1}{\gamma}}
\label{eq:TTt_ppt}
\end{equation}
\begin{equation}
\frac{\rho}{\rho_{t}} = \left ( \frac{p}{p_{t}} \right )^{\frac{1}{\gamma}}
\label{eq:rrt_ppt}
\end{equation}
Ausgedrückt als Funktion der Machzahl \(Ma\) lauten die Beziehungen wie folgt:
\begin{equation}
\frac{p}{p_{t}} = \left ( 1 + \frac{\gamma-1}{2} Ma^{2} \right )^{\frac{-\gamma}{\gamma-1}}
\label{eq:ppt_Ma}
\end{equation}
\begin{equation}
\frac{T}{T_{t}} = \left ( 1 + \frac{\gamma-1}{2} Ma^{2} \right )^{-1}
\label{eq:TTt_Ma}
\end{equation}
\begin{equation}
\frac{\rho}{\rho_{t}} = \left ( 1 + \frac{\gamma-1}{2} Ma^{2} \right )^{\frac{-1}{\gamma-1}}
\label{eq:rrt_Ma}
\end{equation}
Ausströmen aus einem Behälter
Nachfolgende Abbildung gibt einen qualitativen Verlauf der Machzahl \(Ma=f(p/p_{t})\) beim stationären Ausströmen aus einem Behälter. Um ein stationäres Ausströmen zu gewährleisten, ist ein sehr großer Behälter notwendig, dessen Totalzustand sich im betrachteten Zeitraum nicht ändert.
Wenn der Umgebungsdruck \(p_{amb}\) kleiner ist als der kritische Druck \(p^{*}\), so liegt am Ausströmrand der Düse Überschall vor. In dieem Fall ist eine konvergent-divergente Düse (Laval-Düse) erforderlich, bei der im engsten Querschnitt der kritische Zustand, also \(Ma=1\), vorherrscht. Für Luft mit \(\gamma=1,4\) ergeben sich folgende Werte im kritischen Zustand:
\begin{equation}
\frac{p^{*}}{p_{t}} = \left ( \frac{2}{\gamma + 1} \right )^{\frac{\gamma}{\gamma – 1}} = 0,528
\label{eq:p_crit_air}
\end{equation}
\begin{equation}
\frac{T^{*}}{T_{t}} = \frac{2}{\gamma + 1} = 0,833
\label{eq:T_crit_air}
\end{equation}
\begin{equation}
\frac{\rho^{*}}{\rho_{t}} = \left ( \frac{2}{\gamma + 1} \right )^{\frac{1}{\gamma – 1}} = 0,634
\label{eq:rho_crit_air}
\end{equation}
Nachfolgende Abbildung gibt eine grafische Darstellung verschiedener Größen in Abhängigkeit des Druckverhältnisses \(p/p_{t}\).
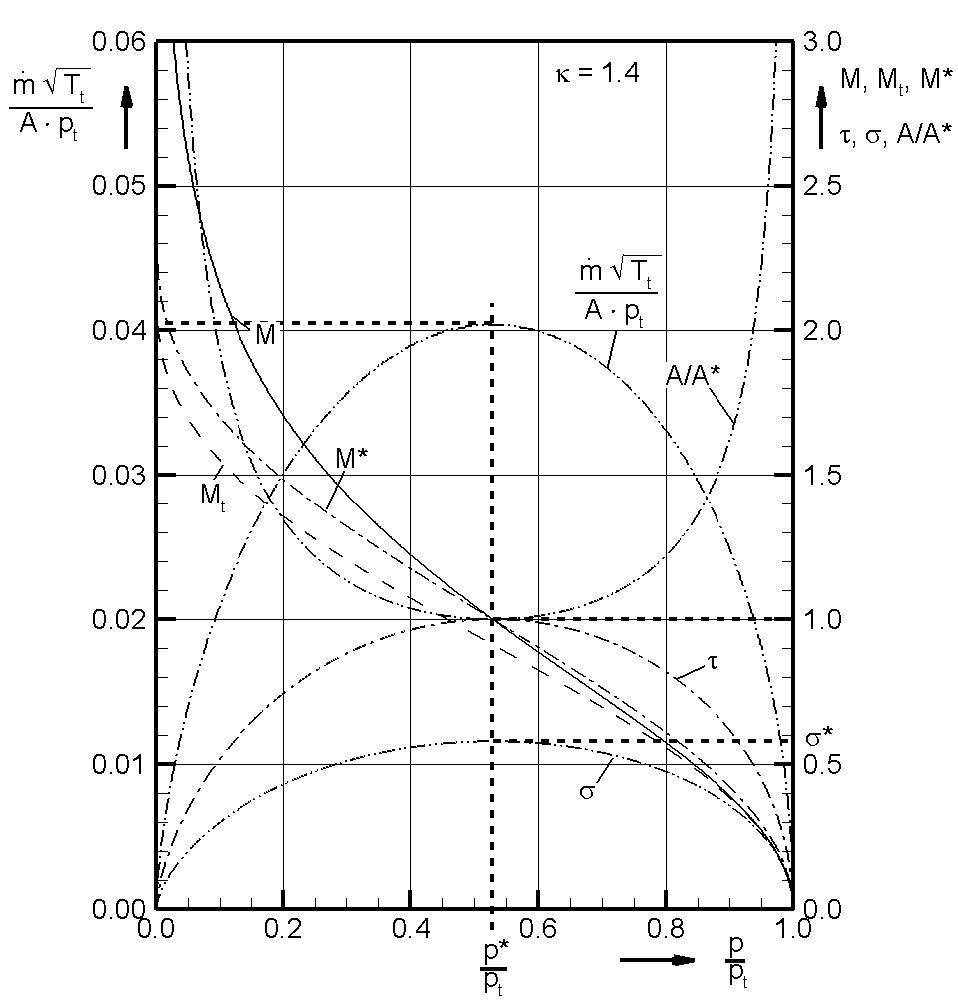
Reduzierte und relative Massenstromdichte
Wird in einer Stromröhre mit veränderlichem Querschnitt der kritische Zustand erreicht, ergibt sich der Massenstrom zu:
\begin{equation}
\dot{m} = \rho^{*} v^{*} A^{*} = \rho^{*} a^{*} A^{*} = \dot{m}_{max}
\label{eq:massfl_crit}
\end{equation}
Auch bei weiterer Absenkung des Gegendrucks bleibt dann der Massenstrom konstant, sofern der Totalzustand vor der Stromröhre unverändert bleibt. Da bei einer stationären Strömung der gleiche Massenstrom an jeder Stelle der Stromröhre vorhanden ist:
\begin{equation}
\dot{m} = \rho v A = \rho^{*} a^{*} A^{*}
\label{eq:massfl_massfl}
\end{equation}
lässt sich unter Verwendung der kompressiblen Beziehungen eine Gleichung für den Querschnitt in Abhängigkeit des Druckverhältnisses herleiten:
\begin{equation}
\frac{A}{A^{*}} = \left ( \frac{2}{\gamma+1} \right )^{\frac{\gamma+1}{2\left( \gamma-1 \right)}} \frac{1}{\left ( \frac{p}{p_{t}} \right )^{\frac{1}{\gamma}} \sqrt{\frac{2}{\gamma-1} \left [ 1- \left ( \frac{p}{p_{t}} \right )^{\frac{\gamma-1}{\gamma}} \right ] }}
\label{eq:AAcrit_ppt}
\end{equation}
Somit ist jedem belibigen Druckverhältnis \(p/p_{t}\) ein bestimmtes Flächenverhältnis \(A/A^{*}\) zugeordnet, so dass man für einen angenommenen Verlauf des Druckverhältnisses (oder der Machzahl) eine Kontur des Strömungskanals, z.B. einer Düse, ermitteln kann.
Die Erweiterung des Massenstroms
\begin{equation}
\dot{m} = \rho v A
\label{eq:massfl_general}
\end{equation}
mit \(\rho^{*}\), \(a^{*}\) und \(\rho_{t}\) führt auf:
\begin{equation}
\dot{m} = \frac{\rho}{\rho^{*}} \frac{v}{a^{*}} A a^{*} \frac{\rho^{*}}{\rho_{t}} \rho_{t}
\label{eq:massfl_erweitert}
\end{equation}
Nun wird die reduzierte Massenstromdichte \(\tau\) definiert zu:
\begin{equation}
\tau = \frac{\rho v}{\rho^{*} a^{*}} = \frac{\textrm{Massenstromdichte}}{\textrm{kritische Massenstromdichte}}
\label{eq:red_massfldens}
\end{equation}
Vergleicht man diese Definition mit Gl. \eqref{eq:massfl_massfl}, ergibt sich der Zusammenhang:
\begin{equation}
\tau = \frac{1}{\frac{A}{A^{*}}}
\label{eq:tau_A}
\end{equation}
und ferner über die Gl. \eqref{eq:AAcrit_ppt} der Zusammenhang zwischen \(\tau\) und \(p/p_{t}\).
Unter Verwendung der kritischen Größen nach Gln. \eqref{eq:p_crit}, \eqref{eq:T_crit} und \eqref{eq:rho_crit} lässt sich der Massenstrom wie folgt schreiben:
\begin{equation}
\dot{m} = \tau A \left ( \frac{2}{\gamma+1} \right )^{\frac{1}{\gamma – 1}} \sqrt{\frac{2 \gamma}{\gamma + 1} R_{i} T_{t}} \frac{p_{t}}{R_{i} T_{t}}
\label{eq:massfl_critvals}
\end{equation}
\begin{equation}
\frac{\dot{m} \sqrt{T_{t}}}{p_{t} A} = \tau \left ( \frac{2}{\gamma+1} \right )^{\frac{\gamma+1}{2\left ( \gamma – 1 \right ) }} \sqrt{\frac{\gamma}{R_{i}}}
\label{eq:massfl_critvals2}
\end{equation}
Nach Einführung der Konstanten \(K\):
\begin{equation}
K = \left ( \frac{2}{\gamma+1} \right )^{\frac{\gamma+1}{2\left ( \gamma – 1 \right ) }} \sqrt{\frac{\gamma}{R_{i}}}
\label{eq:constK}
\end{equation}
erhält man die relative Massenstromdichte:
\begin{equation}
\frac{\dot{m} \sqrt{T_{t}}}{p_{t} A} = \tau K
\label{eq:rel_massfldevs}
\end{equation}
Da \(\tau\) nur vom Druckverhältnis \(p/p_{t}\) abhängig ist, ist auch die relative Massenstromdichte nur eine Funktion von \(p/p_{t}\). Die Konstante \(K\) hängt nur von den Stoffeigenschaften ab.
Bei kritischem Zustand ist \(\tau=1\), da hierfür \(\rho=\rho^{*}\) und \(v=a^{*}\) sind. Es folg somit für den kritischen Zustand:
\begin{equation}
\frac{\dot{m} \sqrt{T_{t}}}{p_{t} A} = K
\label{eq:rel_mfd_crit}
\end{equation}
Die relative Massenstromdichte ist bei kritischem Zustand konstant.
Unter Verwendung der Gln. \eqref{eq:AAcrit_ppt} und \eqref{eq:tau_A} ergibt sich:
\begin{equation}
\frac{\dot{m} \sqrt{T_{t}}}{p_{t} A} = \sqrt{\frac{\gamma}{R_{i}}} \left ( \frac{p}{p_{t}} \right )^{\frac{1}{\gamma}} \sqrt{\frac{2}{\gamma-1} \left [ 1- \left ( \frac{p}{p_{t}} \right )^{\frac{\gamma-1}{\gamma}} \right ] }
\label{eq:rel_mfd2}
\end{equation}
Analog zur reduzierten Massenstromdichte \(\tau\) nach Gl. \eqref{eq:red_massfldens} läßt sich eine weitere reduzierte Massenstromdichte \(\sigma\) definieren:
\begin{equation}
\sigma= \frac{\rho v}{\rho_{t} a_{t}} = \frac{\textrm{Massenstromdichte}}{\textrm{Gesamtmassenstromdichte}}
\label{eq:red_massfldens_sigma}
\end{equation}
Nach Verwendung der Beziehungen für \(Ma_{t}\) und \(\rho/\rho_{t}\) in Abhängigkeit von \(p/p_{t}\) folgt:
\begin{equation}
\sigma= \frac{\rho v}{\rho_{t} a_{t}} = \left ( \frac{p}{p_{t}} \right )^{\frac{1}{\gamma}} \sqrt{\frac{2}{\gamma-1} \left [ 1 – \left ( \frac{p}{p_{t}} \right )^{\frac{\gamma-1}{\gamma}} \right ]}
\label{eq:red_massfldens_sigma2}
\end{equation}
Demnach ist auch die gasdynamische Funktion \(\sigma\) nur vom Druckverhältnis \(p/p_{t}\) und vom Isentropenexponenten \(\gamma\) abhängig.
Der Vergleich zu Gl. \eqref{eq:rel_mfd2} führt auf eine Beziehung zwischen der relativen Massenstromdichte und \(\sigma\):
\begin{equation}
\frac{\dot{m} \sqrt{T_{t}}}{p_{t} A} = \sigma \sqrt{\frac{\gamma}{R_{i}}}
\label{eq:rel_mfd_sigma}
\end{equation}