Mit dem Wirkungsgrad wird eine Aussage darüber getroffen, wie effizient die Energieumwandlung durchgeführt wird. Hierbei kann man verschiedene Abschnitte der Energiewandlungskette betrachten, wodurch sich verschiedene Wirkungsgrade ergeben. Für den Triebwerksbau sind folgende von besonderem Interesse:
- Gesamtwirkungsgrad
- Vortriebswirkungsgrad
- Thermischer Wirkungsgrad
Gesamtwirkungsgrad
Bei diesem Wirkungsgrad wird die gesamte Energiewandlungskette betrachtet, d.h. es wird der dem Luftstrom zugeführte Wärmestrom \(\dot{Q}\) als Einstieg genommen und die Schubleistung \(P_{F}\) als letztes Glied der Energiewandlung:
\begin{equation}
\eta_{all} = \frac{P_{F}}{\dot{Q}} = \frac{\textrm{Schubleistung}}{\textrm{zugeführter Wärmestrom}}
\label{eq:eta_all_general}
\end{equation}
Die Schubleistung ergibt sich aus:
\begin{equation}
P_{F} = F v_{0}
\label{eq:thrust_power}
\end{equation}
und der durch die vollständige Verbrennung des Treibstoffs zugeführte Wärmestrom:
\begin{equation}
\dot{Q} = \dot{m}_{f} h_{low}
\label{eq:added_heat}
\end{equation}
Hierbei bezeichnet \(h_{low}\) den unteren Heizwert des Treibstoffs. Dieser Wert kann als spezifische Enthalpie betrachtet werden und entspricht der gravimetrischen Energiedichte. Für Kerosin:
\begin{equation}
h_{low} = 43 \frac{MJ}{kg}
\label{eq:hlow_kerosene}
\end{equation}
Um einen Zwischenschritt in der Energiewandlung zu betrachten, kann der Gesamtwirkungsgrad mit der Strahlleistung \(P_{j}\) erweitert werden:
\begin{equation}
\eta_{all} = \frac{P_{F}}{\dot{Q}} = \frac{P_{F}}{P_{j}} \frac{P_{j}}{\dot{Q}} = \eta_{p} \eta_{th}
\label{eq:eta_all_extended}
\end{equation}
mit:
\begin{equation}
P_{j}= \frac{1}{2} \left ( \dot{m}_{e} v_{e}^{2} – \dot{m}_{i} v_{0}^{2} \right )
\label{eq:jet_power}
\end{equation}
\begin{equation}
P_{j}= \frac{1}{2} \dot{m}_{i} \left [ \left (1 + f \right ) v_{e}^{2} – v_{0}^{2} \right ]
\label{eq:jet_power2}
\end{equation}
Mit der Vereinfachung \(f \ll 1\) bzw. \(\dot{m}_{e} \approx \dot{m}_{i} = \dot{m}\) ergibt sich daraus:
\begin{equation}
P_{j}= \frac{1}{2} \dot{m} \left ( v_{e}^{2} – v_{0}^{2} \right )
\label{eq:jet_power_simpl}
\end{equation}
In Gl. \eqref{eq:eta_all_extended} sind bereits der Vortriebswirkungsgrad \(\eta_{p}\) und der thermische Wirkungsgrad \(\eta_{th}\) eingeführt worden. Demnach wird der zugeführte Wärmestrom zunächst in die Strahlleistung umgewandelt und anschließend die Strahlleistung in die Schubleistung.
Thermischer Wirkungsgrad
Mit dieser Kennzahl wird die Güte der Umwandlung des zugeführten Wärmestroms in die Strahlleistung beurteilt:
\begin{equation}
\eta_{th} = \frac{P_{j}}{\dot{Q}}
\label{eq:eta_th_general}
\end{equation}
Mit Gln. \eqref{eq:added_heat} und \eqref{eq:jet_power_simpl} ergibt sich:
\begin{equation}
\eta_{th} = \frac{1}{2} \frac{\left ( v_{e}^{2} – v_{0}^{2} \right )}{f h_{low}}
\label{eq:eta_th_simpl}
\end{equation}
Diese Gleichung gilt für ein Triebwerk mit nur einem Luftstrom, also für den Turbojet. Eine Erweiterung auf Turbofans ist durch die separate Berechnung der beiden Luftströme und anschließende Summation möglich.
Vortriebswirkungsgrad
Im nächsten Schritt der Energiewandlung wird die Strahlleistung in die Schubleistung umgewandelt, woraus sich die Definition des Vortriebswirkungsgrads ableitet:
\begin{equation}
\eta_{p} = \frac{P_{F}}{P_{j}}
\label{eq:eta_p_general}
\end{equation}
Einsetzen der Gln. \eqref{eq:thrust_power} und \eqref{eq:jet_power_simpl} führt auf:
\begin{equation}
\eta_{p} = \frac{F v_{0}}{\frac{1}{2} \dot{m} \left ( v_{e}^{2} – v_{0}^{2} \right )}
\label{eq:eta_p_2}
\end{equation}
Mit der vereinfachten Schubgleichung:
\begin{equation}
F = \dot{m} \left ( v_{e} – v_{0} \right )
\label{eq:thrust_simplified}
\end{equation}
ergibt sich:
\begin{equation}
\eta_{p} = \frac{\dot{m} \left ( v_{e} – v_{0} \right ) v_{0}}{\frac{1}{2} \dot{m} \left ( v_{e}^{2} – v_{0}^{2} \right )} = \frac{ \left ( v_{e} – v_{0} \right ) v_{0}}{\frac{1}{2} \left ( v_{e}^{2} – v_{0}^{2} \right )}
\label{eq:eta_p_3}
\end{equation}
Anwendung der dritten binomischen Formel:
\begin{equation}
v_{e}^{2} – v_{0}^{2} = \left ( v_{e} + v_{0} \right ) \left ( v_{e} – v_{0} \right )
\label{eq:binom_3}
\end{equation}
führt auf:
\begin{equation}
\eta_{p} = \frac{2 v_{0}}{v_{e} + v_{0}}
\label{eq:eta_p_4}
\end{equation}
\begin{equation}
\eta_{p} = \frac{2}{1 + \frac{v_{e}}{v_{0}}}
\label{eq:eta_p_simpl}
\end{equation}
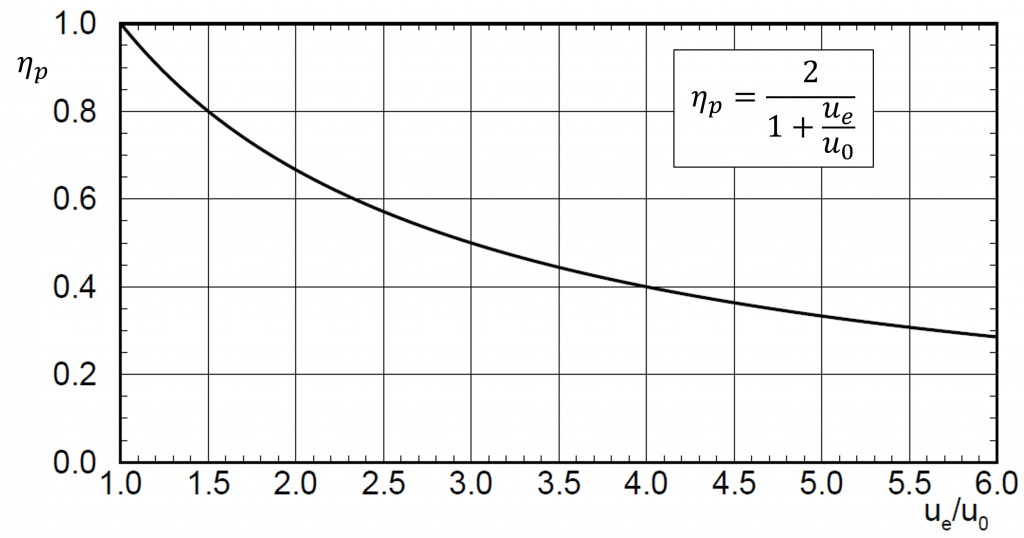
Dieses einfache Ergebnis ist auch nur auf den Turbojet anwendbar. Da die Strahlgeschwindigkeit \(v_{e}\) immer größer sein muss als die Fluggeschwindigkeit \(v_{0}\), um Schub zu erzeugen, wird sofort ersichtlich, dass der Nenner immer größer ist als der Zähler, demnach ist der Vortriebswirkungsgrad immer kleiner als 1 (bzw. <100%). Nachfolgende Abbildung gibt eine grafische Auswertung der Gl. \eqref{eq:eta_p_simpl}, aus der ersichtlich wird, dass zunehmende Strahlgeschwindigkeit zu einem abnehmenden Vortriebswirkungsgrad führt. Aus diesem Grund ist eine Erhöhung der Strahlgeschwindigkeit ungünstig. Unter Berücksichtigung dieses Aspektes kann die vereinfachte Schubgleichung \eqref{eq:thrust_simplified} neu interpretiert werden. Als eine geeignete Maßnahme zur Schubsteigerung bleibt nur noch die Erhöhung des Massenstroms übrig. Mit anderen Worten, es ist günstiger, großen Massenstrom nur wenig zu beschleunigen als umgekehrt. Eine wichtige technologische Konsequenz aus diesem Zusammenhang ist der Trend zu immer größeren Nebenstromverhältnissen (BPR – bypass ratio).